Medidas de tendencia central
Las medidas de tendencia central son valores que se ubican al centro de un conjunto de datos ordenados según su magnitud. Generalmente se utilizan 4 de estos valores también conocidos como estadifico la media aritmética, la mediana, la moda.
MEDIA ARITMÉTICA:
Es la medida de posición utilizada con más frecuencia.
Si se tienen valores de observaciones, la media aritmética es la suma de todos y caca uno de los valores dividida entre el total de valores: Lo que indica que puede ser afectada por los valores extremos, por lo que puede dar una imagen distorsionada de la información de los datos también es el valor obtenido por la suma de todos sus valores dividida entre el número de su mandos.
La media aritmética es, probablemente, uno de los parámetros estadísticos más extendidos.
Se le llama también promedio o, simplemente, media.
Es la medida de posición utilizada con más frecuencia.
Si se tienen valores de observaciones, la media aritmética es la suma de todos y caca uno de los valores dividida entre el total de valores: Lo que indica que puede ser afectada por los valores extremos, por lo que puede dar una imagen distorsionada de la información de los datos también es el valor obtenido por la suma de todos sus valores dividida entre el número de su mandos.
La media aritmética es, probablemente, uno de los parámetros estadísticos más extendidos.
Se le llama también promedio o, simplemente, media.
FORMULA
Dado un conjunto numérico de datos, x1, x2, ..., xn, se define su media aritmética como;

- PROPIEDADES
- Las principales propiedades de la media aritmética son:
- Su cálculo es muy sencillo y en él intervienen todos los datos.
- Su valor es único para una serie de datos dada.
- Se usa con frecuencia para comparar poblaciones, aunque es más apropiado acompañarla de una medida de dispersión.
- Se interpreta como "punto de equilibrio" o "centros de masa" del conjunto de datos, ya que tiene la propiedad de equilibrar las desviaciones de los datos respecto de su propio valor:
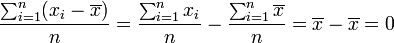 MEDIANA:Es el valor que ocupa la posición central en un conjunto de datos, que deben estar ordenados, de esta manera la mitad de las observaciones es menor que la mediana y la otra mitad es mayor que la mediana, resulta muy apropiada cuando se poseen observaciones extremas.La mediana, representa el valor de la variable de posición central en un conjunto de datos ordenadosCALCULO
MEDIANA:Es el valor que ocupa la posición central en un conjunto de datos, que deben estar ordenados, de esta manera la mitad de las observaciones es menor que la mediana y la otra mitad es mayor que la mediana, resulta muy apropiada cuando se poseen observaciones extremas.La mediana, representa el valor de la variable de posición central en un conjunto de datos ordenadosCALCULO
Es el valor medio en un conjunto de valores ordenados. Corresponde al perceptibles 50 o segundo cuadrante (P50 o Q2). Los pasos son:- Ordena los valores en orden del menor al mayor
- Cuenta de derecha a izquierda, o al revés, hasta encontrar el valor o valores medios.
Ejemplo: tenemos el siguiente conjunto de números 8,3,7,4,11,2,9,4,10,11,4 ordenamos: 2,3,4,4,4,7,8,9,10,11,11 En esta secuencia la mediana es 7, que es el número central. Y si tuviésemos: 8,3,7,4,11,9,4,10,11,4, entonces ordenamos: 3,4,4,4,7,8,9,10,11,11 y la mediana (Md) está en: los números centrales son 7 y 8, lo que haces Existen dos métodos para el cálculo de la mediana:- Considerando los datos en forma individual, sin agruparlos.
- Utilizando los datos agrupados en intervalos de clase
Sean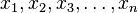 los datos de una muestra ordenada en orden creciente y designando la mediana como
los datos de una muestra ordenada en orden creciente y designando la mediana como 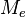 , distinguimos dos casos:
, distinguimos dos casos:
a) Si n es impar, la mediana es el valor que ocupa la posición una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir:
una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir: 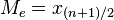 .Por ejemplo, si tenemos 5 datos, que ordenados son:
.Por ejemplo, si tenemos 5 datos, que ordenados son: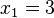 ,
, 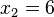 ,
, 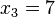 ,
, 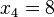 ,
, 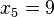 => El valor central es el tercero:
=> El valor central es el tercero: 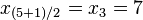 . Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo (
. Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo ( ,
,  ) y otros dos por encima de él (
) y otros dos por encima de él ( ,
,  ).
).
b) Si n es par, la mediana es la media aritmética de los dos valores centrales. Cuando es par, los dos datos que están en el centro de la muestra ocupan las posiciones
es par, los dos datos que están en el centro de la muestra ocupan las posiciones  y
y 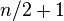 . Es decir:
. Es decir: 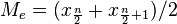 .Por ejemplo, si tenemos 6 datos, que ordenados son:
.Por ejemplo, si tenemos 6 datos, que ordenados son: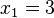 ,
, 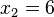 ,
, 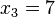 ,
, 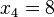 ,
, 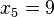 ,
, 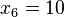 => Hay dos valores que están por debajo del
=> Hay dos valores que están por debajo del 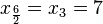 y otros dos que quedan por encima del siguiente dato
y otros dos que quedan por encima del siguiente dato  . Por tanto, la mediana de este grupo de datos es la media aritmética de estos dos datos:
. Por tanto, la mediana de este grupo de datos es la media aritmética de estos dos datos: 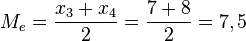 .MODAEs el valor de un conjunto de datos que aparece con mayor frecuencia. No depende de valores extremos, pero es más variables que la media y la mediana. La moda es el valor con una mayor frecuencia en una distribución de datos
.MODAEs el valor de un conjunto de datos que aparece con mayor frecuencia. No depende de valores extremos, pero es más variables que la media y la mediana. La moda es el valor con una mayor frecuencia en una distribución de datos
Hablaremos de una distribución bimodal de los datos adquiridos en una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. Si todas las variables tienen la misma frecuencia diremos que no hay moda.El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:Siendo la frecuencia absoluta del intervalo modal las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal.


No hay comentarios:
Publicar un comentario