Medidas de dispercion
Estudia la distribución de los valores de la serie, analizando si estos se encuentran más o menos concentrados, o más o menos dispersos.
Existen diversas medidas de dispersión, entre las más utilizadas podemos destacar las siguientes:
1.- Rango: mide la amplitud de los valores de la muestra y se calcula por diferencia entre el valor más elevado y el valor más bajo.
2.- Varianza: Mide la distancia existente entre los valores de la serie y la media. Se calcula como sumatorio de las difrencias al cuadrado entre cada valor y la media, multiplicadas por el número de veces que se ha repetido cada valor. El sumatorio obtenido se divide por el tamaño de la muestra.
La varianza siempre será mayor que cero. Mientras más se aproxima a cero, más concentrados están los valores de la serie alrededor de la media. Por el contrario, mientras mayor sea la varianza, más dispersos están.3.- Desviación típica: Se calcula como raíz cuadrada de la varianza.
4.- Coeficiente de varización de Pearson: se calcula como cociente entre la desviación típica y la media.

Observaciones sobre la varianza
La varianza, al igual que la media, es un índice muy sensible a las puntuaciones extremas.
En los casos que no se pueda hallar la media tampoco será posible hallar la varianza.
La varianza no viene expresada en las mismas unidades que los datos, ya que las desviaciones están elevadas al cuadrado.
DIVISIÓN ESTÁNDAR
La desviación estándar o desviación típica es la raíz cuadrada de la varianza.
Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
La desviación estándar se representa por σ.

EJERCICIO
9, 3, 8, 8, 9, 8, 9, 18
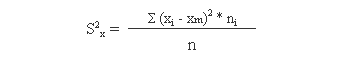

No hay comentarios:
Publicar un comentario